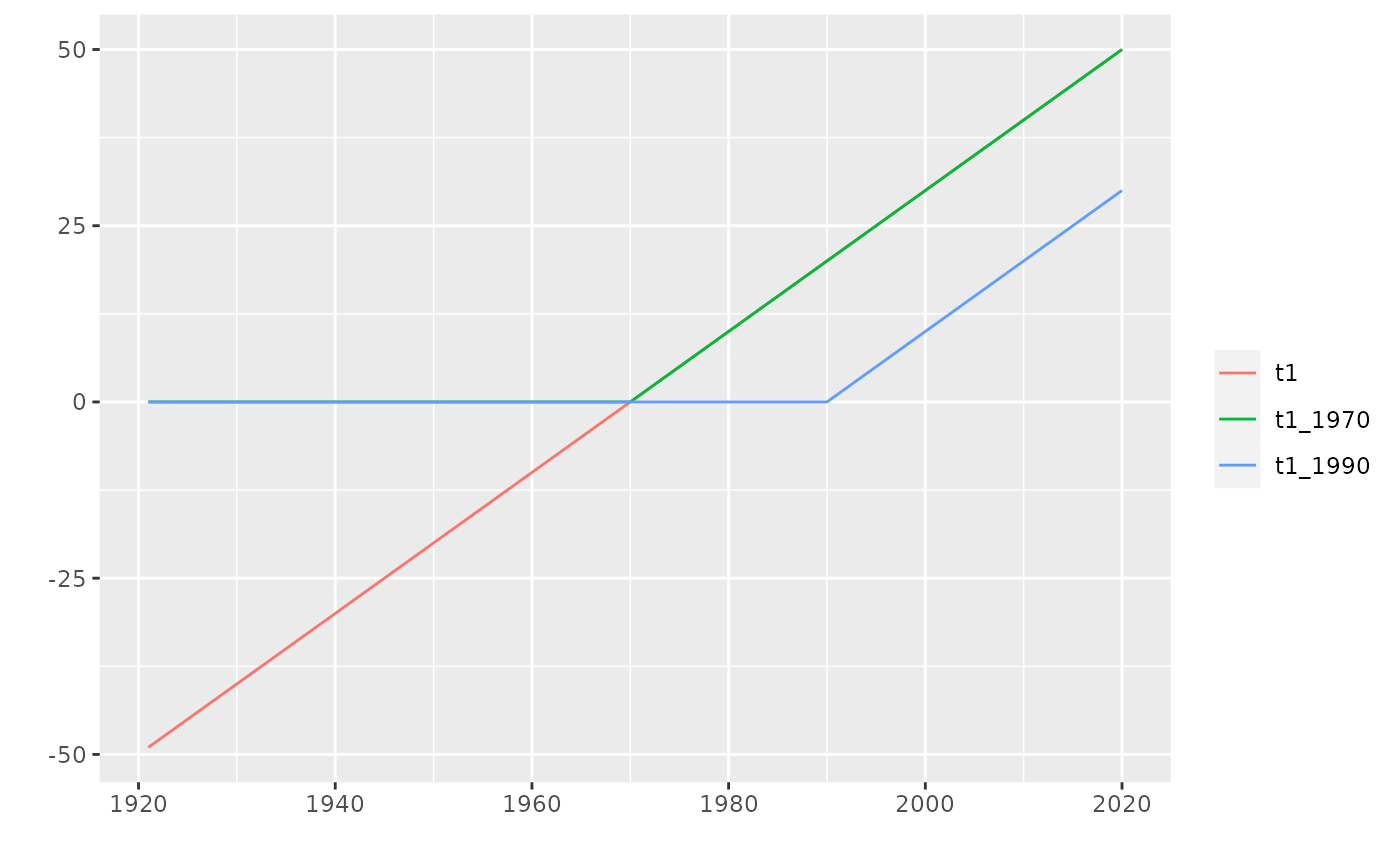
Design Matrix with Breaks in a Linear Trend

Build a design matrix to describe breaks in a linear trend.

breaksX(date, degree = 1L, origin = NULL, breaks = NULL, constant = FALSE)

Arguments

date: A vector with class "Date" or a vector that can be coerced to the "Date" class, typically an unambiguous character vector.
degree: The degree used for spline functions.
origin: Not used yet.
breaks: A vector describing the breaks. It will be coerced to the "Date" class, and can be e.g. an unambigous character vector.
constant: Logical. If TRUE a column with constant unit value is added.

Value

An object of class "bts" inheriting from "matrix". This is essentially a numeric matrix with the value of the basis functions as its columns. The rows are in correspondence with the elements of the date vector given on input.

Details

The design matrix is a Truncated Power Basis of splines. It can be extended to a degree differing from the default value \(1\). The provided date is converted into a numeric variable \(t\) corresponding to the number of years from the origin. The basis functions are functions of this variable \(t\). A year is defined as 365.25 days, so \(t\) can not take only integer values.

Consider the date as a numeric variable \(t\), let \(d\) be the degree. The basis consist in

the powers \(t^0 = 1\), \(t^1\), \(\dots\), \(t^d\) where \(d\) is the given degree.
the truncated powers \((t - \tau_k)^d_+\) where \(\tau_k\) is the break with number \(k\) and \(x_+\) is the positive part of \(x\) (so \(x_+ = 0\) when \(x < 0\)).

The power zero will be discarded when constant is FALSE.

Note

When the argument breaks has length zero, the function returns a polynomial basis with the constant possibly removed.

Author

Yves Deville

Examples


date <- as.Date(sprintf("%4d-01-01", 1921:2020)) 
X1 <- breaksX(date = date, breaks = c("1970-01-01", "1990-01-01"))
plot(X1)