Methods computing spacings between Largest Order Statistics

Methods computing the random spacings for the Largest Order Statistics of the marks in a POT renewal.

Usage

spacings(object, ...)

# S3 method for numeric
spacings(object, wExp = TRUE, ...)

# S3 method for data.frame
spacings(object, varName, wExp = TRUE, ...)

# S3 method for Rendata
spacings(object, type = c("MAX", "OTS", "OT"), wExp = TRUE, ...)

Arguments

object

A object containing the marks \(X_i\). This is can be a vector or a data frame for data aggregated by blocks. For an object of class data.frame one of the three data.frame slots: OTdata, MAXdata or OTSdata can be used using the suitable value of type.

varName

Character vector of length 1 giving the name of the variable when object is a data.frame.

wExp

Logical. If TRUE, the spacings are weighted as explained in Details.

type

Character specifying the data.frame to be used when object has class "Rendata".

...

Not used yet.

Details

The spacings are the differences between the Largest Order Statistics. They are useful for some estimation tasks or diagnostics. Given random variables \(X_i\), the \(i\)-th spacing \(Y_i\) is the difference \(X_{(i)}-X_{(i+1)}\) between the \(i\)-th largest order statistic \(X_{(i)}\) and the next in the decreasing order i.e. \(X_{(i+1)}\).

When the r.vs \(X_i\) form a sample of an exponential or Gumbel distribution, the spacings associated with the largest order statistics are or tend to be independent and exponentially distributed. More precisely, the weighted spacings \(i \times Y_i\) have or tend to have the same exponential distribution. This can be used to estimate the shape parameter of the underlying distribution using only the largest order statistics. Moreover the \(r-1\) spacings \(Y_i\) built from the \(r\) largest order statistics \(i \le r\) are or tend to be independent from the \(r\)-th largest order statistic \(X_{(r)}\).

When wExp is TRUE, the returned values are the weighted spacings \(i \times Y_i\).

Value

A list or vector containing the spacings. When the data is structured in blocks as is the MAXdata slot of an object of class

"Rendata", the spacings are computed form the order statistics

within each block, to maintain independence with the next order statistic in decreasing order.

References

Embrechts P., Klüppelberg C. and Mikosch T. (1997) Modelling Extremal Events for Insurance and Finance. Springer.

Author

Yves Deville

Caution

By default, the spacings are scaled as explained above, thus assuming that the marks are exponentially distributed.

Examples

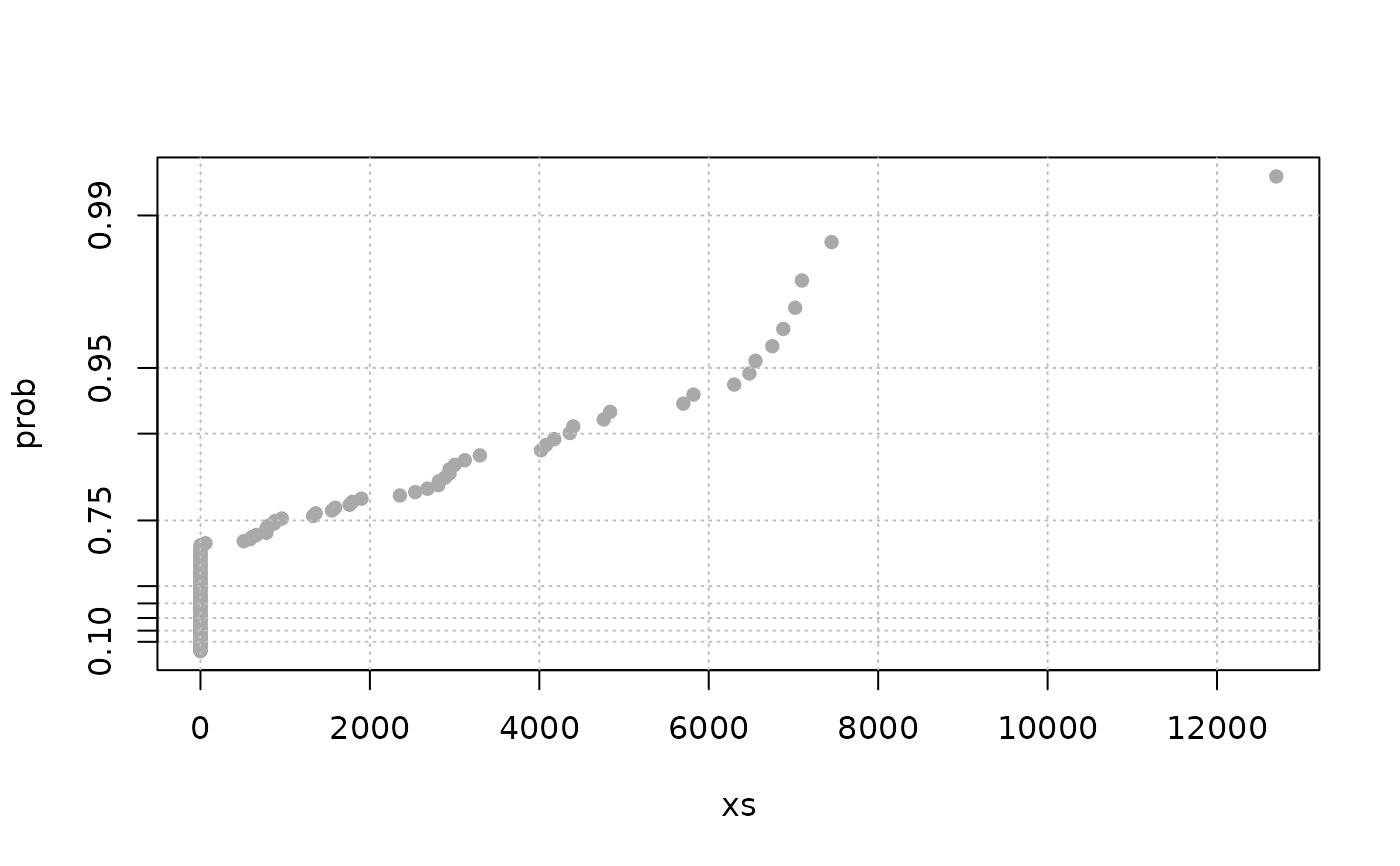
sp <- spacings(rgumbel(200, loc = 0, scale = 1))
expplot(sp)

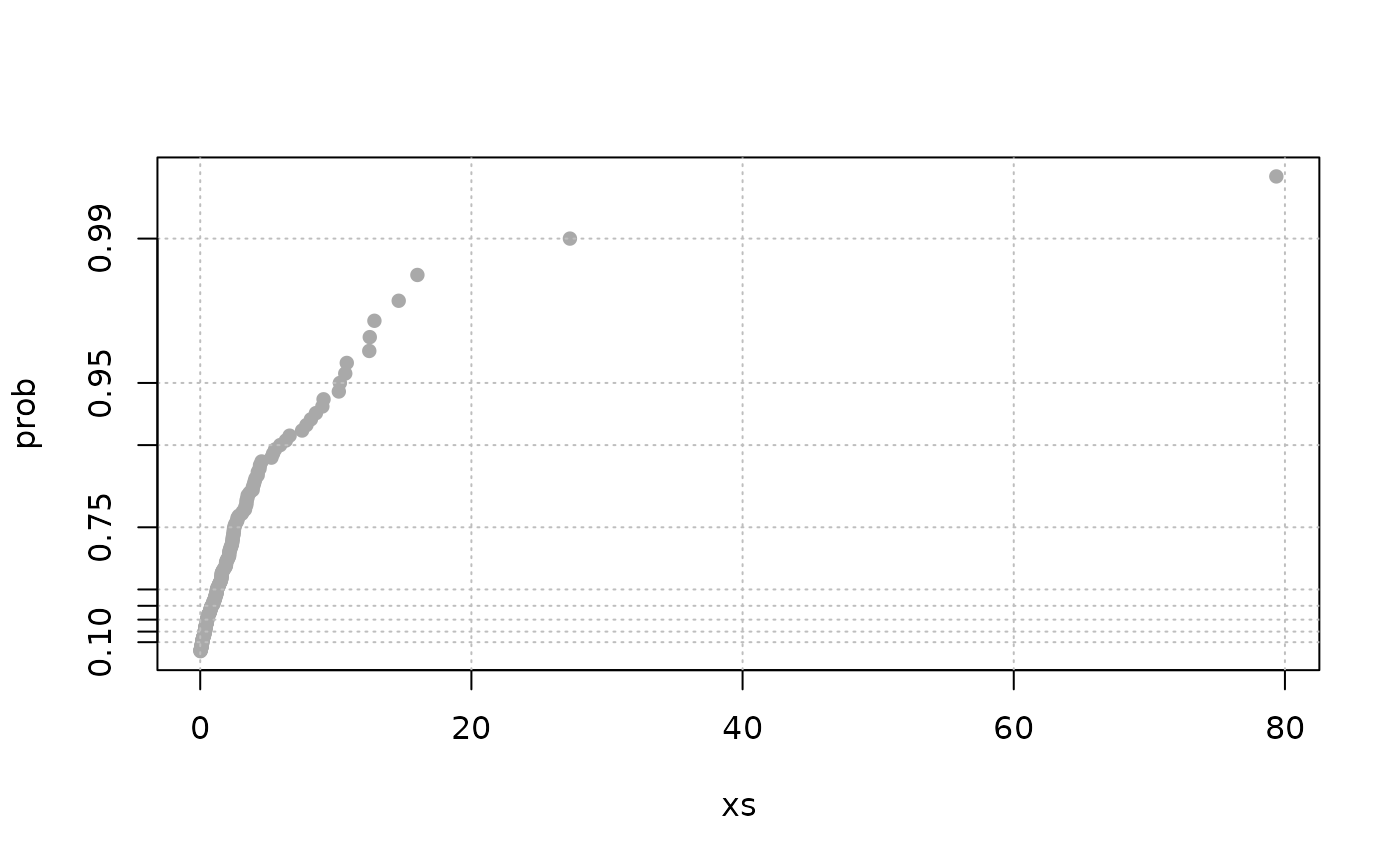sp1 <- spacings(rgev(200, loc = 0, scale = 1, shape = 0.3))
expplot(sp1)

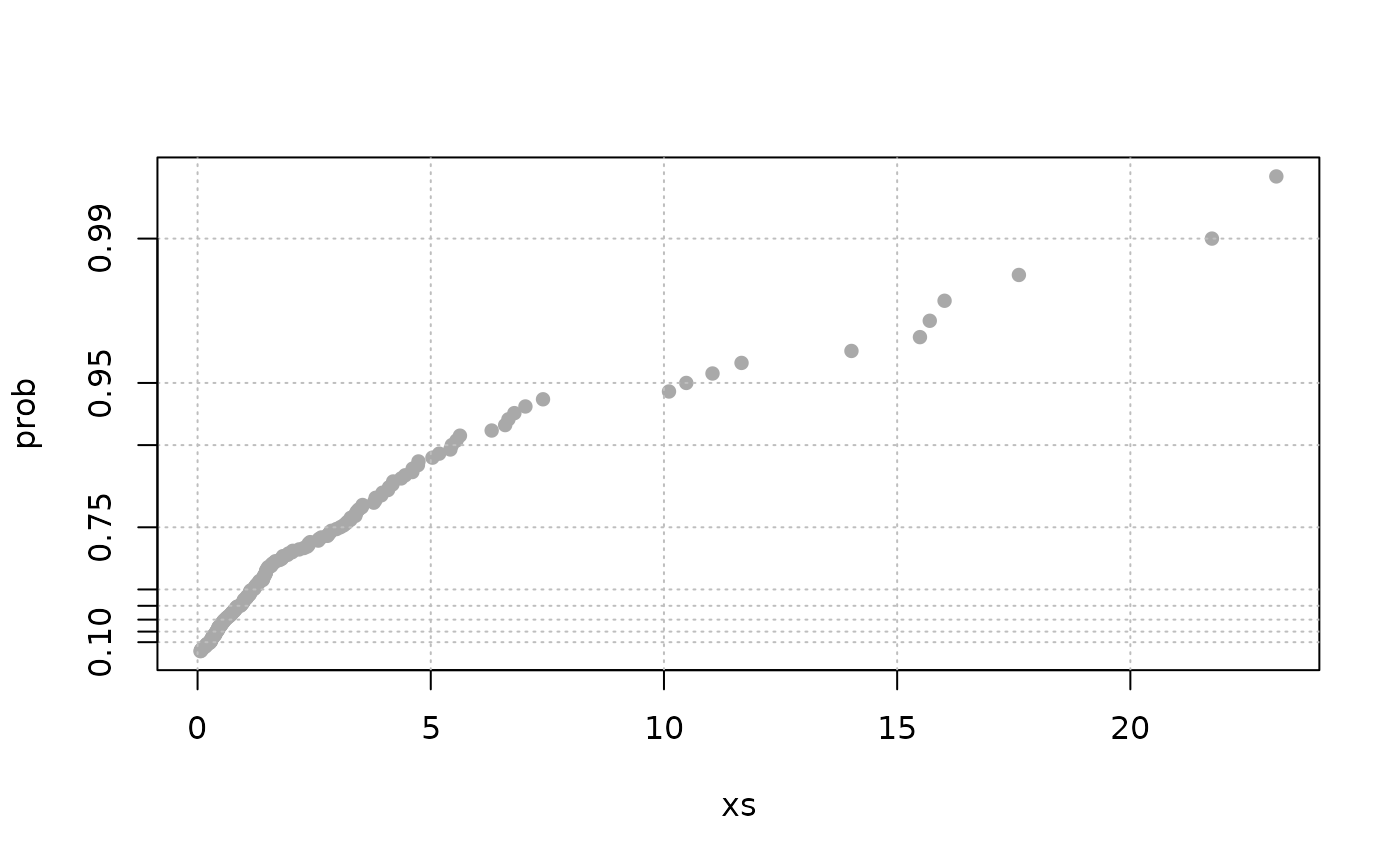## spacings are computed by block
sp2 <- spacings(object = Garonne$MAXdata,
                varName = Garonne$info$varName)
expplot(unlist(sp2))

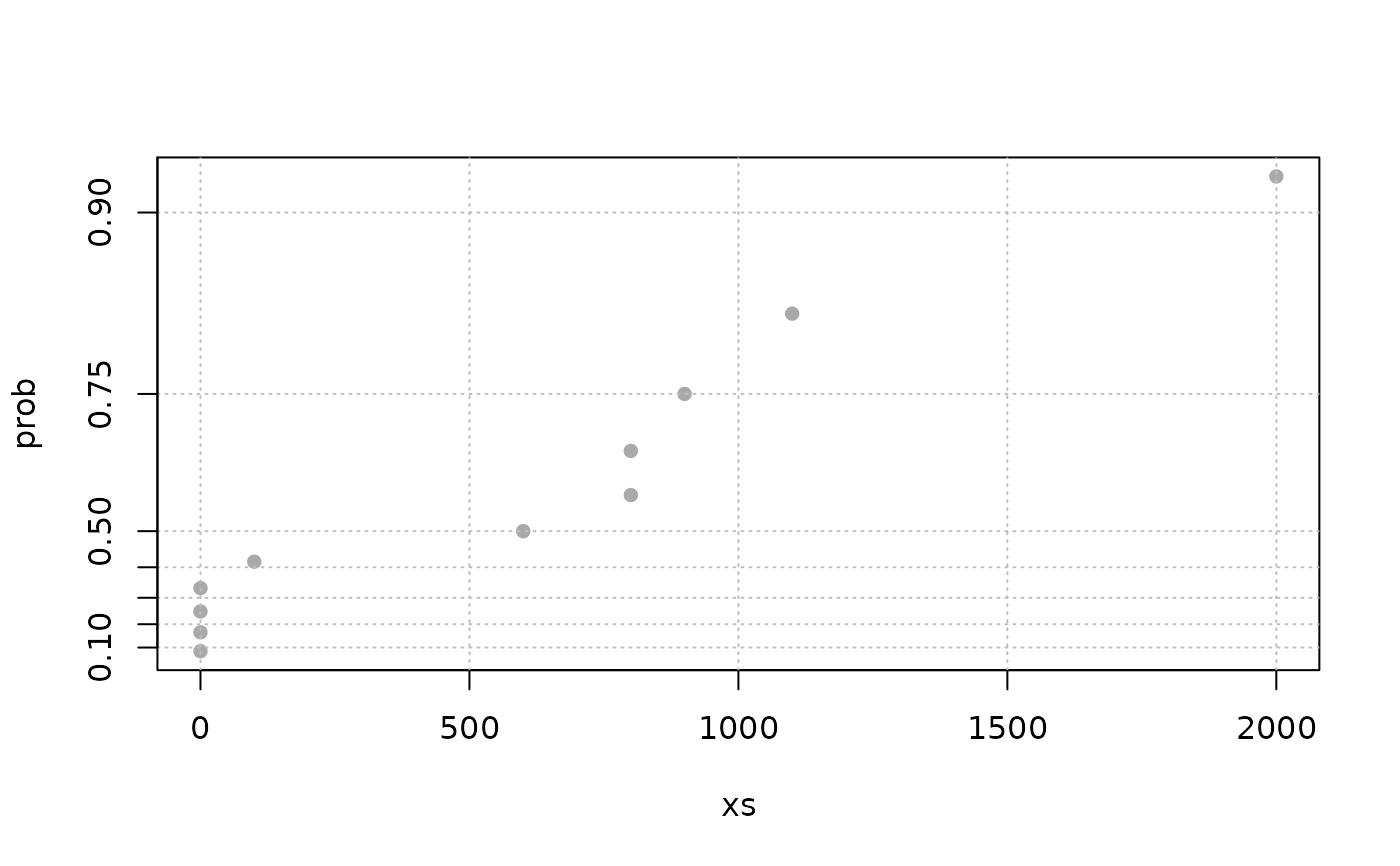sp3 <- spacings(object = Garonne, type = "OT")
expplot(sp3)