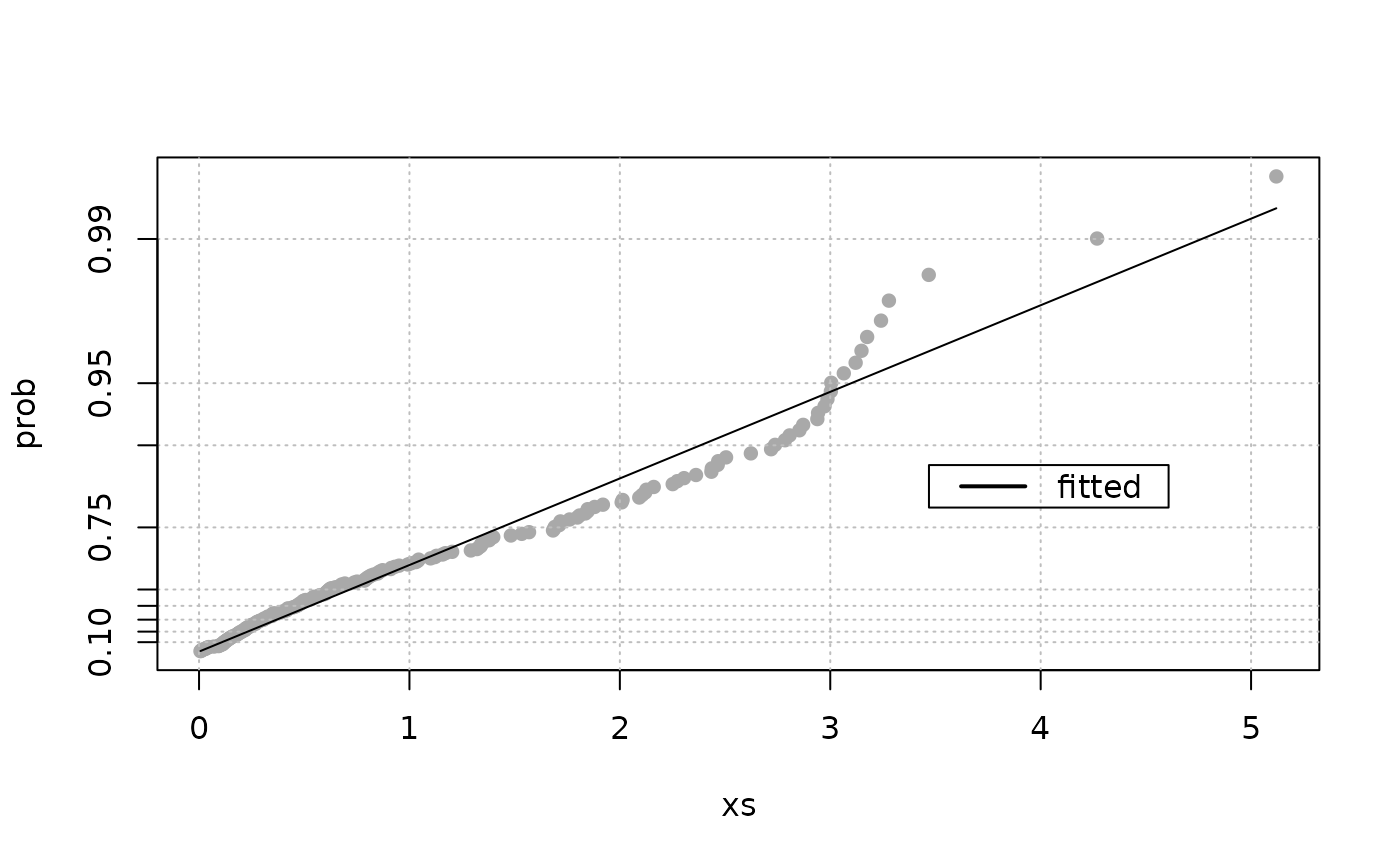
Classical "exponential distribution" plot

Plot a vector using "exponential distribution" scales

Usage

expplot(x,
        plot.pos = "exp",
        rate = NULL,
        labels = NULL,
        mono = TRUE,
        ...)

Arguments

x

The vector to be plotted.

plot.pos

Plotting position for points: either "exp" for expected ranks or "med" for a median rank approximation (see Details below).

rate

Rate parameter for one or several "exponential distribution" lines to be plotted

labels

Text to display in legend when "exponential distribution" lines are specified

mono

Monochrome graph?

...

Arguments to be passed to plot.

Details

This plot shows \(-\log[1-F(x)]\) against \(x\) where \(F(x)\) at point \(i\) is taken as \(i/(n+1)\) if plot.pos is "exp", or as the "median rank" approximation \((i-0.3)/(n+0.4)\) if plot.pos is "med".

If the data in x is a sample from an exponential distribution, the points should be roughly aligned. However the largest order statistics have high sampling dispersion.

Author

Yves Deville

Note

The log scale for y is emulated via the construction of suitable graduations. So be careful when adding graphical material (points, etc) to this graph with functions of the "add to plot" family (points, lines, ...).

The ML estimate of the rate parameter is the inverse of the sample mean.

See also

The weibplot function for a classical "Weibull" plot. The interevt is useful to compute interevents (or "interarrivals") that should follow an exponential distribution in the homogeneous Poisson process context.

Examples

 x <- rexp(200)
 expplot(x, rate = 1/mean(x), labels = "fitted")