Skip to contents

ML estimation of classical Weibull distribution

fweibull.Rd

Fast Maximum Likelihood estimation of the classical two parameters Weibull distribution.

Usage

fweibull(x, info.observed = TRUE, scaleData = TRUE, cov = TRUE,
         check.loglik = FALSE)

Arguments

x

Sample vector to be fitted. Should contain only positive non-NA values.

info.observed

Should the observed information matrix be used or the expected one be used?

scaleData

Should the data be scaled before estimation? If TRUE, the observations in x (which are positive) are divided by their mean value. The results are in theory not affected by this transformation, but scaling the data could improve the estimation in some cases.

cov

Should the covariance of estimates be computed?

check.loglik

If TRUE, the log-likelihood is recomputed using dweibull function with log = TRUE. The result is returned as a list element.

Details

The ML estimates are obtained thanks to a reparameterisation with \(\eta = scale^{1/shape}\) in place of shape. This allows the maximisation of a one-dimensional likelihood \(L\) since the \(\eta\) parameter can be concentrated out of \(L\). This also allows the determination of the expected information matrix for \([shape,\,\eta]\) rather than the usual observed information.

Value

A list

estimate

Parameter ML estimates.

sd

The (asymptotic) standard deviation for estimate.

cov

The (asymptotic) covariance matrix computed from theoretical or observed Information matrix.

eta

The estimated value for eta.

Author

Yves Deville

Note

The default value of info.observed was set to TRUE from version 3.0-1 because standard deviations obtained with this choice are usually better.

See also

weibplot for Weibull plots.

Examples


n <- 1000
set.seed(1234)
shape <- 2 * runif(1)
x <- 100 * rweibull(n, shape = 0.8, scale = 1)
res <- fweibull(x)

## compare with MASS
if (require(MASS)) {
   res2 <- fitdistr(x , "weibull")
   est <- cbind(res$estimate, res2$estimate)
   colnames(est) <- c("Renext", "MASS")
   loglik <- c(res$loglik, res2$loglik)
   est <- rbind(est, loglik)
   est
}
#>               Renext          MASS
#> shape      0.7690861     0.7690905
#> scale     96.5701573    96.5741808
#> loglik -5659.0502224 -5659.0502229

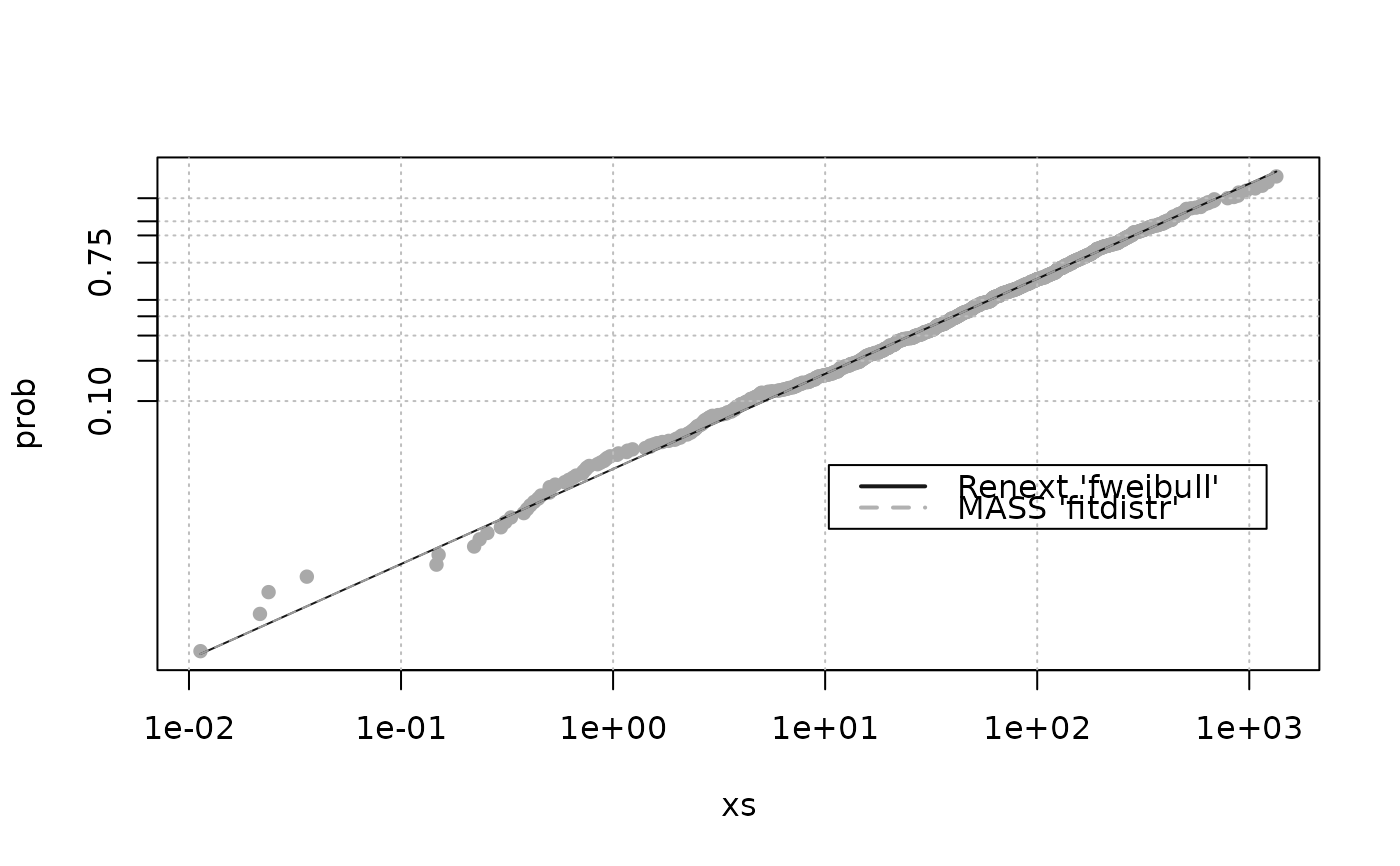
## Weibull plot
weibplot(x,
         shape = c(res$estimate["shape"], res2$estimate["shape"]),
         scale = c(res$estimate["scale"], res2$estimate["scale"]),
         labels = c("Renext 'fweibull'", "MASS 'fitdistr'"),
         mono = TRUE)