Negative Binomial Levy process

Negative Binomial Lévy process estimation from partial observations (counts)

Usage

NBlevy(N,
       gamma = NA,
       prob = NA,
       w = rep(1, length(N)),
       sum.w = sum(w),
       interval = c(0.01, 1000),
       optim = TRUE,
       plot = FALSE, ...)

Arguments

N

Vector of counts, one count by time period.

gamma

The gamma parameter if known (NOT IMPLEMENTED YET).

prob

The prob parameter if known (NOT IMPLEMENTED YET).

w

Vector of time length (durations).

sum.w

NOT IMPLEMENTED YET. The effective duration. If sum.w is strictly inferior to sum(w), it is to be understood that missing periods occur within the counts period. This can be taken into account with a suitable algorithm (Expectation Maximisation, etc.)

interval

Interval giving min and max values for gamma.

optim

If TRUE a one-dimensional optimisation is used. Else the zero of the derivative of the (concentrated) log-likelihood is searched for.

plot

Should a plot be drawn? May be removed in the future.

...

Arguments passed to plot.

Details

The vector $\mathbf{N}$ contains counts for events occurring on non-overlapping time periods with lengths given in $\mathbf{w}$. Under the NB Lévy process assumptions, the observed counts (i.e. elements of $\mathbf{N}$) are independent random variables, each following a negative binomial distribution. The size parameter $r_k$ for $N_k$ is $r_k = \gamma w_k$ and the probability parameter $p$ is prob. The vector $\boldsymbol{\mu}$ of the expected counts has elements $$\mu_k=\mathrm{E}(N_k)=\frac{1-p}{p} \,\gamma \,w_k.$$

The parameters $\gamma$ and $p \:(\code{prob})$ are estimated by Maximum Likelihood using the likelihood concentrated with respect to the prob parameter.

Value

A list with the results

estimate

Parameter estimates.

sd

Standard deviation for the estimate.

score

Score vector at the estimated parameter vector.

info

Observed information matrix.

cov

Covariance matrix (approx.).

References

Kozubowski T.J. and Podgórsky K. (2009) "Distributional properties of the negative binomial Lévy process". Probability and Mathematical Statistics 29, pp. 43-71. Lund University Publications.

Author

Yves Deville

Note

The Negative Binomial Lévy process is an alternative to the Homogeneous Poisson Process when counts are subject to overdispersion. In the NB process, all counts share the same index of dispersion (variance/expectation ratio), namely 1/prob. When prob is close to 1, the counts are nearly Poisson-distributed.

Examples

## known parameters
nint <- 100
gam <- 6; prob <- 0.20

## draw random w, then the counts N
w <- rgamma(nint, shape = 3, scale = 1/5)
N <- rnbinom(nint, size = w * gam, prob = prob)
mu <- w * gam * (1 - prob) / prob
Res <- NBlevy(N = N, w = w)

## Use example data 'Brest'
## compute the number of event and duration of the non-skipped periods
gof1 <- gof.date(date = Brest$OTdata$date,
                 skip = Brest$OTmissing,
                 start = Brest$OTinfo$start,
                 end = Brest$OTinfo$end,
                 plot.type = "omit")

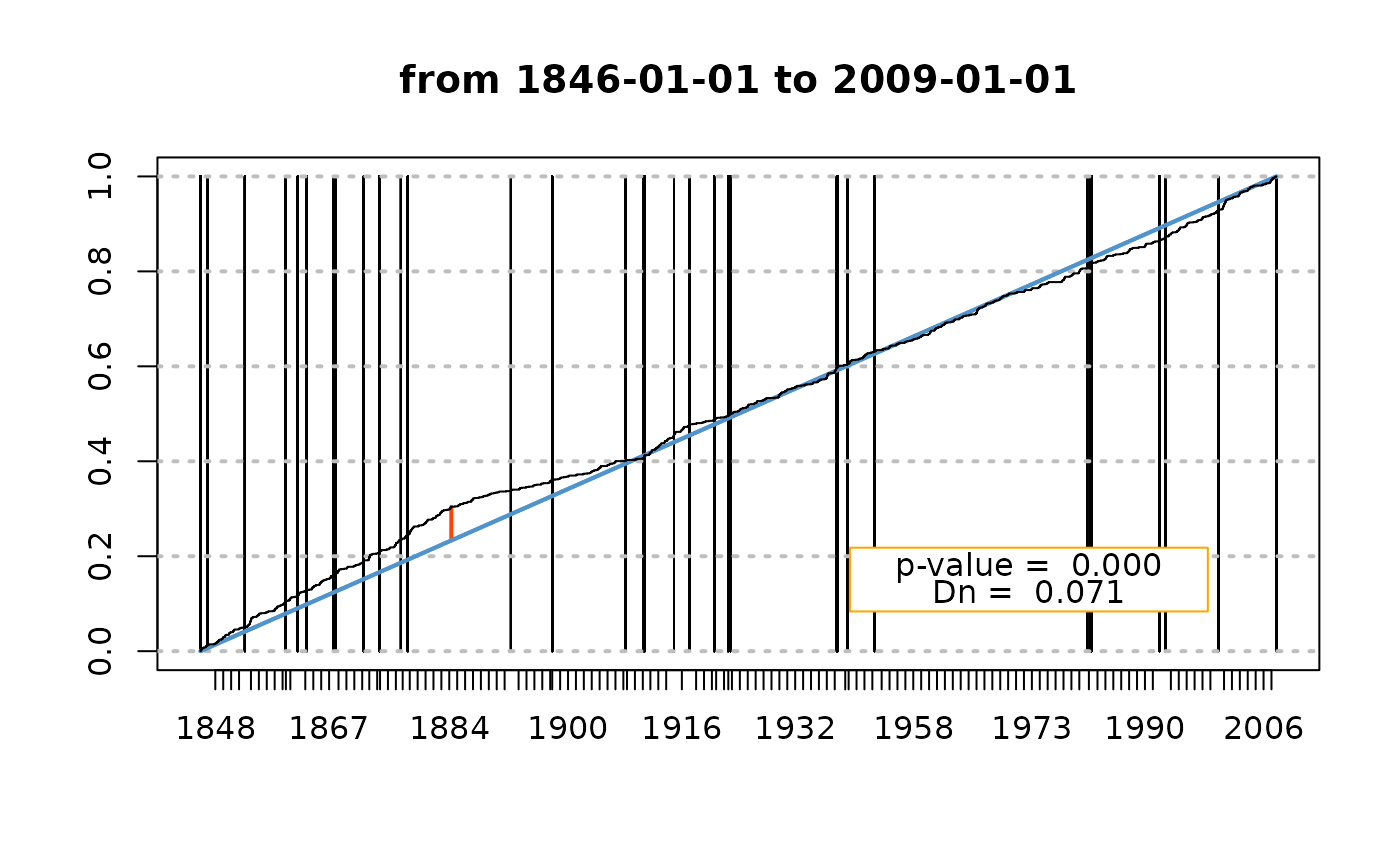ns1 <- gof1$noskip
## fit the NBlevy
fit1 <- NBlevy(N = ns1$nevt, w = ns1$duration)

## use a higher threshold
OT2 <- subset(Brest$OTdata, Surge > 50)
gof2 <- gof.date(date = OT2$date,
                 skip = Brest$OTmissing,
                 start = Brest$OTinfo$start,
                 end = Brest$OTinfo$end,
                 plot.type = "omit")

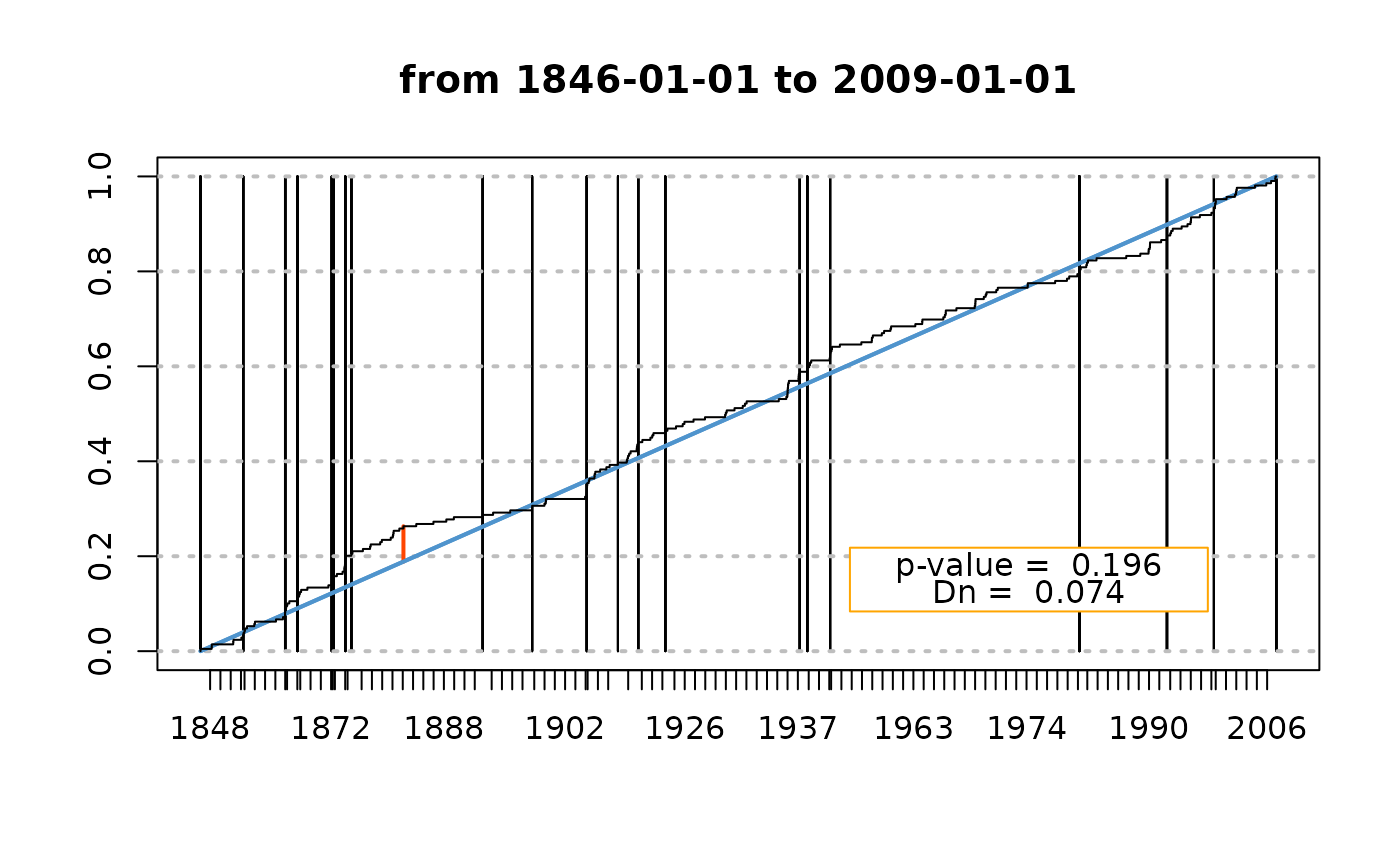ns2 <- gof2$noskip
## the NBlevy prob is now closer to 1
fit2 <- NBlevy(N = ns2$nevt, w = ns2$duration)

c(fit1$prob, fit2$prob)
#> [1] 0.3203404 0.5162115