Generalised Pareto Distribution

Density function, distribution function, quantile function, random generation, hazard and cumulative hazard functions for the Generalised Pareto Distribution.

Usage

dGPD(x, loc = 0.0, scale = 1.0, shape = 0.0, log = FALSE)
   pGPD(q, loc = 0.0, scale = 1.0, shape = 0.0, lower.tail = TRUE)
   qGPD(p, loc = 0.0, scale = 1.0, shape = 0.0, lower.tail = TRUE)
   rGPD(n, loc = 0.0, scale = 1.0, shape = 0.0)
   hGPD(x, loc = 0.0, scale = 1.0, shape = 0.0)
   HGPD(x, loc = 0.0, scale = 1.0, shape = 0.0)

Arguments

x, q

Vector of quantiles.

p

Vector of probabilities.

n

Number of observations.

loc

Location parameter $\mu$.

scale

Scale parameter $\sigma$.

shape

Shape parameter $\xi$.

log

Logical; if TRUE, the log density is returned.

lower.tail

Logical; if TRUE (default), probabilities are $\textrm{Pr}[X <= x]$, otherwise, $\textrm{Pr}[X > x]$.

Details

Let $\mu$, $\sigma$ and $\xi$ denote loc, scale and shape. The distribution values $y$ are $\mu \leq y < y_{\textrm{max}}$.

When $\xi \neq 0$, the survival function value for $y \geq \mu$ is given by

$$S(y) = \left[1 + \xi(y - \mu)/\sigma\right]^{-1/ \xi} \qquad \mu < y < y_{\textrm{max}}$$ where the upper end-point is $y_{\textrm{max}} = \infty$ for $\xi >0$ and $y_{\textrm{max}} = \mu -\sigma/ \xi$ for $\xi <0$.

When $\xi = 0$, the distribution is exponential with survival $$S(y) = \exp\left[- (y - \mu)/\sigma\right] \qquad \mu \leq y. $$

Value

dGPD gives the density function, pGPD gives the distribution function, qGPD gives the quantile function, and

rGPD generates random deviates. The functions

hGPD and HGPD return the hazard rate and the cumulative hazard.

Note

The functions are slight adaptations of the [r,d,p,q]gpd functions in the evd package. The main difference is that these functions return NaN when shape is negative, as it might be needed in unconstrained optimisation. The quantile function can be used with p=0 and p=1, then returning the lower and upper end-point.

Examples

qGPD(p = c(0, 1), shape = -0.2)
#> [1] 0 5
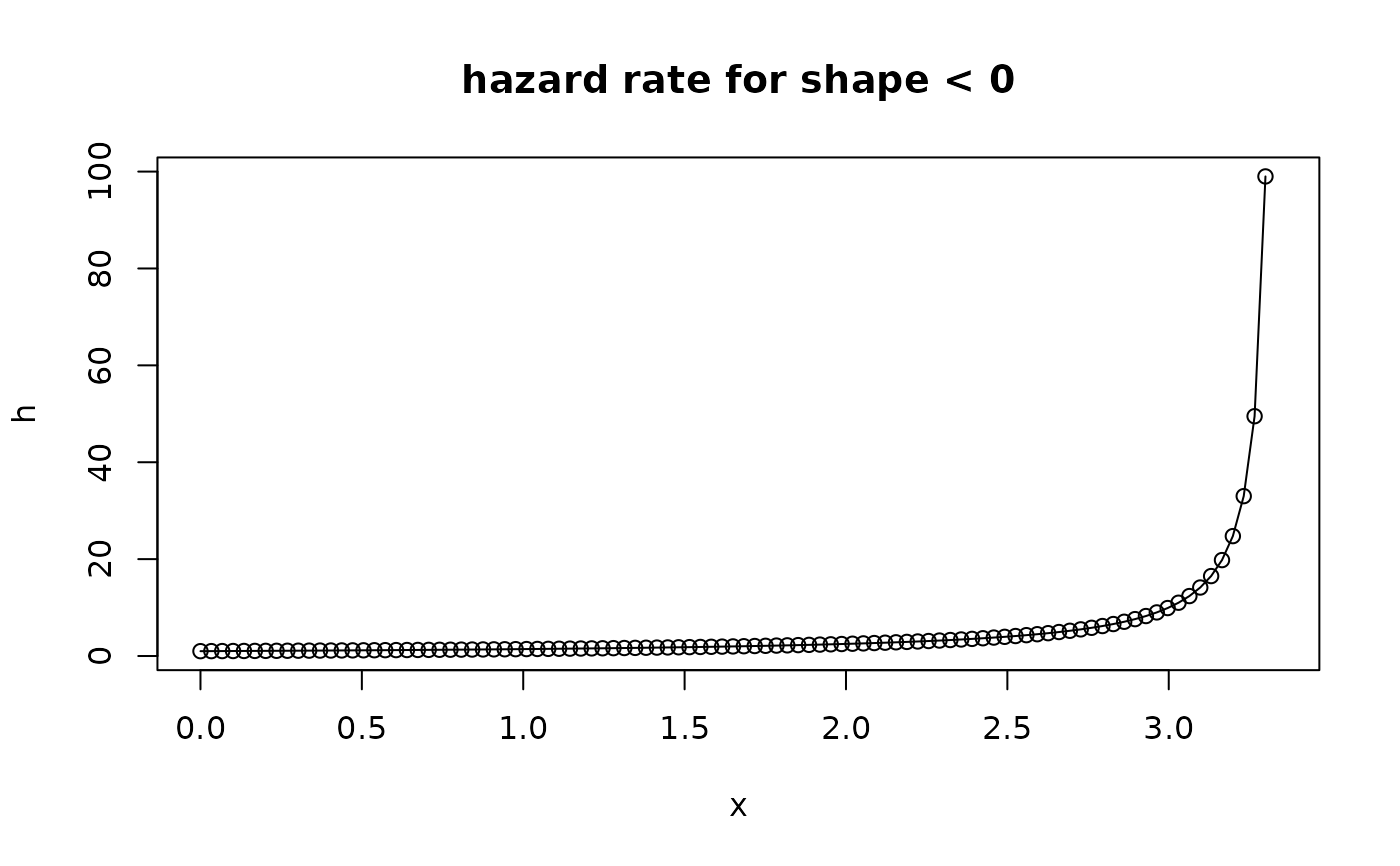
shape <- -0.3
xlim <- qGPD(p = c(0, 1), shape = shape)
x <- seq(from = xlim[1], to = xlim[2], length.out = 100)
h <- hGPD(x, shape = shape)
plot(x, h, type = "o", main = "hazard rate for shape < 0")

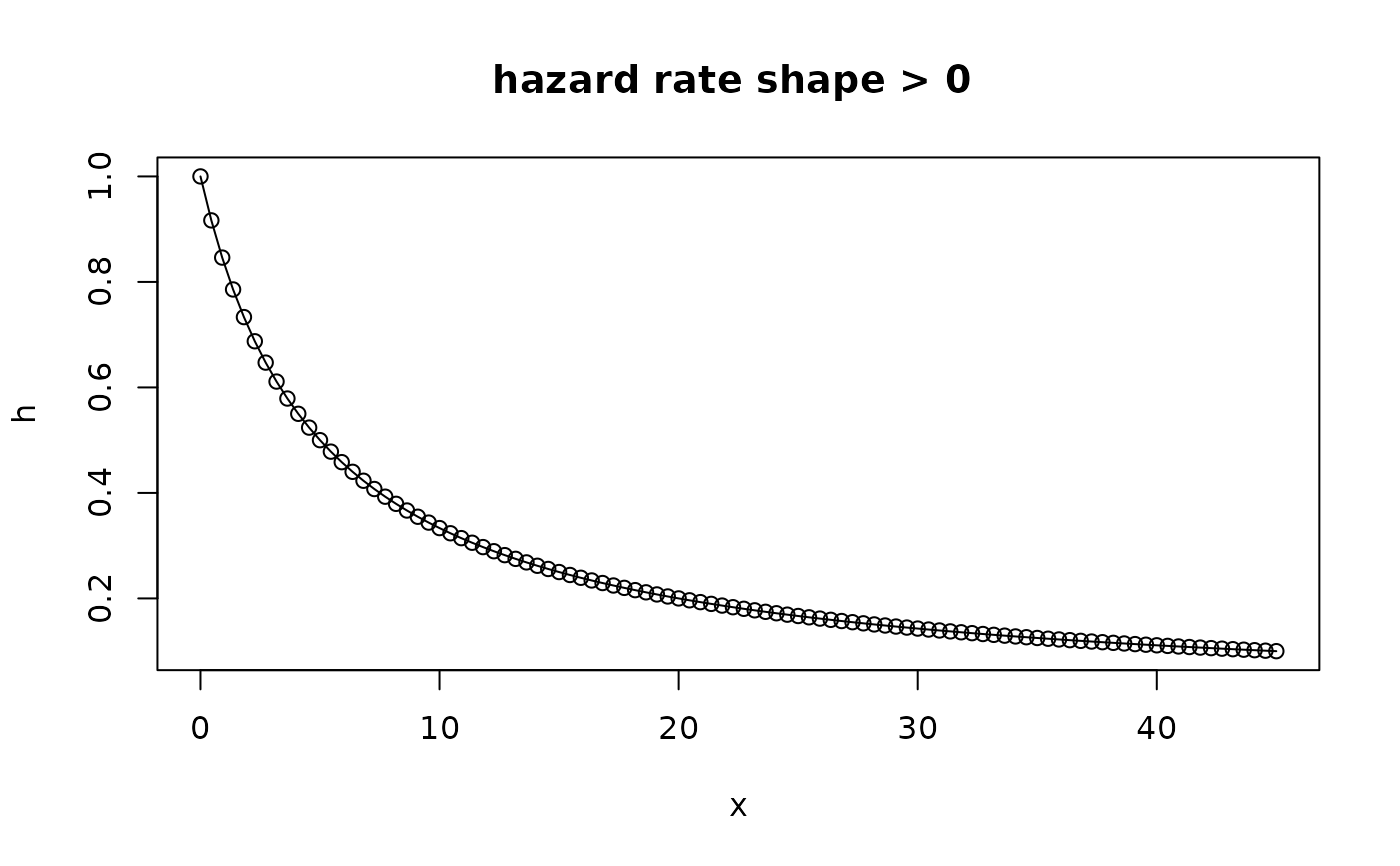
shape <- 0.2
xlim <- qGPD(p = c(0, 1 - 1e-5), shape = shape)
x <- seq(from = xlim[1], to = xlim[2], length.out = 100)
h <- hGPD(x, shape = shape)
plot(x, h, type = "o", main = "hazard rate shape > 0 ")